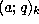defined in the preceding section are called
q-shifted factorials. They can also be defined for negative values of k
as
The symbols 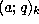defined in the preceding section are called
q-shifted factorials. They can also be defined for negative values of k
as
Now we have
where
We can also define
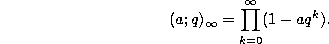
This implies that
and, for any complex number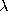 
,
where the principal value of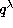 
is taken.
If we change q by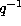 
we obtain
This formula can be used, for instance, to prove the following transformation formula between the little q-Laguerre (or Wall) polynomials given by (3.20.1) and the q-Laguerre polynomials defined by (3.21.1) :
or equivalently
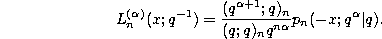
By using (0.2.5) it is not very difficult to verify the following
general transformation formula for 
polynomials (see
section 0.4 for the definition of the basic hypergeometric function
) :
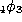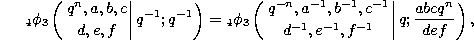
where a limit is needed when one of the parameters is equal to zero. Other transformation formulas can be obtained from this one by applying limits as discussed in section 0.4.
Finally, we list a number of transformation formulas for the q-shifted factorials, where k and n are nonnegative integers :
