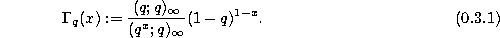
The q-gamma function is defined by
This is a q-analogue of the well-known gamma function since we have

Note that the q-gamma function satisfies the functional equation
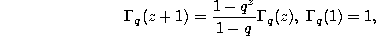
which is a q-extension of the well-known functional equation
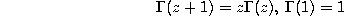
for the ordinary gamma function. For nonintegral values of z this ordinary gamma function also satisfies the relation
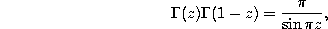
which can be used to show that
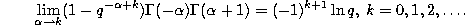
This limit can be used to show that the orthogonality relation (3.27.2) for the Stieltjes-Wigert polynomials follows from the orthogonality relation (3.21.2) for the q-Laguerre polynomials.
The q-binomial coefficient is defined by
where n denotes a nonnegative integer.
This definition can be generalized in the following way. For arbitrary
complex  we have
we have
Or more general for all complex  and
and 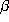 we have
we have
For instance this implies that
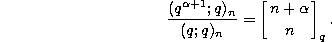
Note that
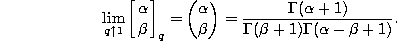
For integer values of the parameter 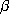 we have
we have
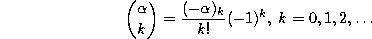
and when the parameter  is an integer too we may write
is an integer too we may write
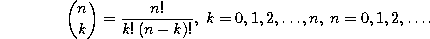
This latter formula can be used to show that

This can be used to write the generating functions (1.8.46) and (1.8.52) for the Chebyshev polynomials of the first and the second kind in the following form :
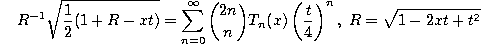
and

respectively.
Finally we remark that