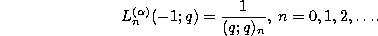One of the most important summation formulas for hypergeometric series is given by the binomial theorem :
A q-analogue of this formula is called the q-binomial theorem :
For 
with n a nonnegative integer we find
In fact this is a q-analogue of Newton's binomium
As an example of the use of these formulas we show how we can obtain the generating function (1.3.12) for the continuous dual Hahn polynomials from the generating function (1.1.12) for the Wilson polynomials. From chapter 2 we know that
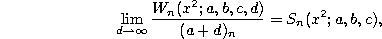
where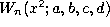 
denotes the Wilson polynomial defined by
(1.1.1) and 
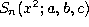denotes the continuous dual Hahn
polynomial given by (1.3.1). Now we have by using
(0..4.6) and (0.5.1)
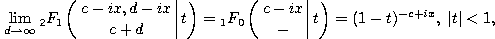
which implies the desired result.
In a similar way we can find the generating function (3.14.11) for the quantum q-Krawtchouk polynomials from the generating function (3.6.11) for the q-Hahn polynomials. First we have from chapter 4 :
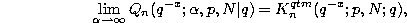
where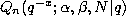 
denotes the q-Hahn polynomial defined by
(3.6.1) and 
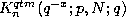denotes the quantum
q-Krawtchouk polynomial given by (3.14.1). Further we
have by using (0.4.9) and (0.5.3)
which leads to the desired result.
Another example of the use of the q-binomial theorem is the proof of the
fact that the generating function (3.10.25) for the continuous
q-ultraspherical (or Rogers) polynomials is a q-analogue of the
generating function (1.8.24) for the Gegenbauer (or
ultraspherical) polynomials. In fact we have, after the substitution
:
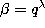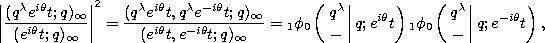
which tends to (for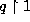 
)
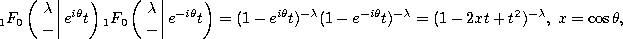
which equals (1.8.24).
The well-known Gauss summation formula
and the Vandermonde summation formula
have the following q-analogues :
and
On the next level we have the summation formula
which is called Saalschütz (or Pfaff-Saalschütz) summation formula. A q-analogue of this summation formula is
Finally, we have a summation formula for the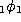 
series :
As an example of the use of this latter formula we remark that the q-Laguerre polynomials defined by (3.21.1) have the property that
