is defined by
The q-derivative operator is defined by
Further we define
It is not very difficult to see that
if the function f is differentiable at z.
An easy consequence of this definition is
for all real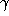 
or more general
Further we have
which is often referred to as the q-product rule. This can be generalized to a q-analogue of Leibniz' rule :
As an example we note that the q-difference equation (3.21.6) of the q-Laguerre polynomials can also be written in terms of this q-derivative operator as
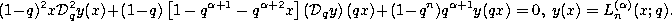
The q-integral is defined by
This definition is due to J. Thomae and F.H. Jackson. Jackson also defined a
q-integral on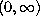 
by
If the function f is continuous on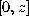 
we have
For instance, the orthogonality relation (3.12.2) for the little q-Jacobi polynomials can also be written in terms of a q-integral as :
